par admin | Nov 10, 2022 | Blog
Description, à l’échelle de la pièce, des effets de l’interaction du laser avec la matière. Approche couche par couche.
On cherche ici à simuler la construction complète de la pièce afin de prédire les distorsions ou les zones de rupture potentielles. Compte tenu des moyens de calculs actuels, plusieurs jours de simulation seraient nécessaire si l’on tenait compte des phénomènes locaux se produisant au sein du bain de fusion et des trajectoires du laser. Afin de rendre ces simulations utilisables par un bureau d’étude, le temps de calcul doit-être le plus court possible et ne doit pas excéder le temps d’impression réel. Les ingénieurs doivent pouvoir vérifier l’imprimabilité de leur pièce dès les premières ébauches jusqu’à la phase finale. Des simplifications doivent donc être faite.

Maillage du domaine occupé par la pièce
La méthode des éléments finis est utilisée ici. Puisque l’on simule l’impression de la pièce complète, il est nécessaire de mailler le domaine complet. La géométrie de la pièce est généralement représentée par un maillage surfacique composé d’éléments triangulaires. Ce maillage représente l’enveloppe externe du volume de la pièce et n’est pas destiné à être utilisé pour la simulation du procédé de fabrication.

Maillage géométrique de la pièce
L’approche la plus courante est de mailler le domaine en couches régulières et d’épaisseur supérieure l’épaisseur réelle de la couche de poudre. C’est le principe adopté par AdditiveLab-RESEARCH. De manière à se focaliser sur le procédé de fabrication, cette étape doit-être robuste, rapide, et automatique. Le maillage voxel répond bien à ces exigences. En contrepartie, la géométrie est comme pixelisée ce qui peut être déroutant d’un premier abord. La projection des résultats sur le maillage géométrique de la pièce permet d’atténuer cet effet par lissage. L’utilisation d’un maillage plus fin est alors plus conditionnée par une recherche de précision que par une meilleure représentation de la surface.
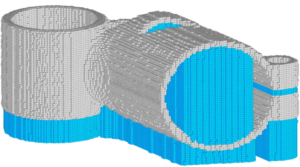
Maillage voxel de la pièce
L’utilisation d’éléments tétraédriques permet de mieux représenter la surface externe. AdditiveLab-RESEARCH ne génère pas de maillage tétra mais il est possible d’importer ce type de maillage. Les voxels demeurent cependant le meilleurs compromis entre robustesse de maillage et précision numérique.
Modélisation du dépôt de matière : activation des éléments :
A l’échelle macroscopique, il n’est pas envisageable de tenir compte de la trajectoire réelle du laser car les temps de calculs seraient rédhibitoires. Le motif imprimé de chaque couche est donc activé en une seule fois. Cette approximation permet d’obtenir des résultats exploitables et utiles. L’approche birth-death est utilisée encore ici. Au début du calcul tous les éléments sont désactivés pour être ensuite réactivés couche par couche au cours du temps pour simuler la déposition de matière. Une couche numérique contient généralement qu’une seule couche d’éléments. Il est cependant possible d’activer plusieurs couches d’éléments à la fois afin de raffiner le maillage sans augmenter le nombre de couches et préserver ainsi le temps de calcul.
Homogénéisation des propriétés de la pièce et des structures supports
Les voxels ne permettent cependant pas de mailler fidèlement les structures fines qui composent les supports (surfaces, barres ou de structures lattices). Les éléments voxels recouvrant ces zones ne sont donc que partiellement remplis de matière. Leur propriétés mécaniques et thermiques doivent alors être adaptées en conséquence. On parle d’homogénéisation des propriétés : un ratio matière/vide est appliqué aux paramètres matériaux associés aux voxels situés dans ces zones.

Voxelization des supports
Simplification des couplages
Les couplages entre phénomènes physiques ajoutent autant de non-linéarités dans la modélisation mathématique du problème augmentant d’autant les temps de calcul. A l’échelle qui nous intéresse ici il est possible de s’affranchir de certains d’entre eux sans affecter la marge de précision attendue.
Dans le couplage thermomécanique à l’échelle macroscopique, la dilatation thermique peut-être considérée comme prépondérante. Cela permet de découpler la résolution de la thermique de celle de la mécanique et de gagner un temps de calcul conséquent.
Simplification de la thermique
Dans le cadre d’une simulation purement thermique, une autre simplification consiste à imposer directement la température de fusion du matériau lors de l’activation de chaque couche. Par conduction, cette température se propage ensuite dans le reste de la pièce. Cela simplifie le problème en le rendant moins non-linéaire d’où un gain de temps.
Bien que moins précise, puisqu’elle ne permet plus de considérer les paramètres machine dans l’évolution réelle de la température, cette simplification permet malgré tout d’identifier, en première approche, les zones nécessitant un refroidissement plus important. Les conclusions obtenues grâce à cette simplification sont ensuite affinées par une approche plus réaliste tenant compte cette fois du flux de chaleur apporté par le laser.
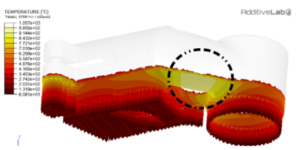
Zone d’accumulation de la chaleur mise en avant par une simulation purement thermique
Simplification du problème thermomécanique
Les contraintes résiduelles et les distorsions sont obtenues par une simulation thermomécanique.
Les résultats d’une simulation thermique détaillée sont couplés avec un modèle mécanique : chaque couche est activée avec la température issue du calcul thermique. L’équilibre statique avec les forces de dilatation induites est calculé après chaque activation de couche.
Ce type de simulation est extrêmement coûteux. Il présente également l’inconvénient de devoir identifier l’évolution en fonction de la température de nombreux paramètres comme la chaleur spécifique, la conduction, le module d’élasticité etc … Ces identifications sont délicates et les mesures diffèrent selon les sources. Cette dépendance en température ajoute également des non-linéarités au problème ralentissant d’autant les temps de calcul.
Ces simulations sont donc plutôt à réservées aux phases intermédiaires et finales du projet afin d’affiner les résultats.
Approche purement mécanique
En simulation du soudage en régime stationnaire (le bain de fusion est établi), on peut considérer en première approximation que les déformations aux abords du bain de fusion ne varient que très peu. En imposant ces déformations au lieu de calculer le temps de calcul est donc très fortement réduit par rapport à une simulation thermodynamique complète. Cette méthode appelée «inherent strain», peut-être transposée à la simulation de la fabrication additive.
Cette déformation inhérente nécessite cependant d’être identifiée. Généralement il est nécessaire d’imprimer un modèle présentant un fort retour élastique après retrait du plateau. La mesure du déplacement vertical permet d’identifier, par méthode inverse les déformations inélastiques responsables du retour élastique observé. Le tenseur de déformation obtenu englobe toutes les déformations inélastiques.
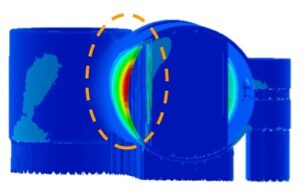
Résultat d’une simulation inherent-strain
Conclusion
La simulation à l’échelle macroscopique est soumise à de nombreuses hypothèses simplificatrices. L’objectif est de réduire au maximum le temps de calcul de manière a explorer de nombreuses configurations d’impression. Une bonne pratique est de déterminer les tendances en commençant par une simulation inherent strain, puis thermique simplifiée avant de passer à la thermique transitoire et enfin à la simulation thermomécanique couplée. L’utilisation d’un maillage grossier dans un premier temps puis des maillages plus fin permet d’itérer rapidement pour identifier les bons paramètres et obtenir une pièce à la bonne cote du premier coup.
par admin | Nov 10, 2022 | Blog
C’est l’échelle des trajectoires laser, assimilable à l’échelle du lit de poudre. Les simulations à l’échelle microscopique permettaient de comprendre en détails le comportement du bain de fusion. L’analyse à l’échelle du cordon permet, quant à elle, d’obtenir des résultats pertinents tels que le manque de fusion, ou les zones d’accumulation de la chaleur.
Les forces régissant le comportement du bain de fusion ne sont pas simulées ici. La température se propage dans la pièce, et éventuellement la poudre avoisinante, par phénomène de conduction. Le coefficient d’absorption est par ailleurs considéré constant. L’évaporation de la matière n’est pas prise en compte tout comme la chaleur latente de changement de phase généralement négligée de manière à réduite les non-linéarités du problème et alléger les temps de calculs.
La poudre étant poreuse, un coefficient de conduction équivalent est calculé. Plusieurs théories existent à ce sujet. Le principe consiste à représenter les grains comme autant de résistances thermiques. La conduction équivalente est alors calculée en considérant un agencement des grains en parallèle ou en série. Ces deux approches permettent en réalité de déterminer les bornes supérieures et inférieures du coefficient de conduction. Des modèles plus élaborés donnent des résultats très précis mais plus coûteux.
Il s’agit d’hypothèses fortes mais qui donnent un bon compromis entre temps de calcul et résultats exploitables par les bureaux d’études. L’objectif peut-être de vérifier que les paramètres machine permettent de fusionner la matière correctement. On peut également vouloir optimiser ces paramètres pour réduire le temps d’impression et de production en général.
Les paramètres concernés sont la vitesse, la puissance, et le diamètre laser, l’épaisseur de couche, l’écart entre deux trajectoires (écart vecteur), éventuellement le temps de « sky writting » lors d’une stratégie de balayage en aller-retour, ainsi que la stratégie de balayage sur plusieurs couches.
L’analyse des dimensions du bain de fusion, permettant de calculer le rapport largeur sur longueur déterminant dans la prédiction de la continuité du cordon, ou des zones n’ayant pas atteint la température de fusion dans le cas d’une analyse multi-trajectoire, permet d’identifier les configurations optimales.
Il peut paraître incohérent de ne pas modéliser la vaporisation d’autant plus que, dans ce cas, la température atteinte dans le bain excède de beaucoup la température de vaporisation, mais l’expérience montre qu’en terme de dimension de bain de fusion, l’erreur commise n’excède pas 10% ce qui est tout à fait raisonnable.
Enfin, l’évolution du bain de fusion n’étant pas modélisée, il est nécessaire de prédéfinir la pénétration du laser selon le mode de fusion souhaité ou attendu. On peut voir cela comme un modèle prédéfini d’évolution du bain de fusion tout comme une loi matériau permet de prédire le comportement des matériaux sans prendre en compte la microstructures. Des résultats incohérents conduiront à un changement de modèle.
Des simulations de plusieurs heures, ou jours selon la longueur de cordon, peuvent ainsi être réduites à quelques heures voire à quelques minutes dans le cas d’un mono-cordon.
par admin | Nov 10, 2022 | Blog
Les phénomènes ayant lieu dans le bain de fusion concernent la matière dans son état solide, liquide ou gazeux. L’objectif est de prédire la forme du bain de fusion, sa stabilité et éventuellement la quantité de gaz matière vaporisée.
Comme pour toute modélisation, l’espace et le temps sont divisés en intervalles. Compte-tenu des mouvements de la matière fondue au sein du bain de fusion, le maillage doit être découplé des mouvements de la matière. Dans le cas contraire, les éléments du maillage seraient distordus, voir retournés ce qui provoquerait l’arrêt des calculs. Les approches lagrangiennes sont donc proscrites au profit des approches eulérienne voire mixte (euler-lagrange).
Les équations régissant la matière dans son état solide, liquide ou gazeux sont utilisés. Aux interfaces de transition d’un état à l’autre, des loi de mélange sont généralement utilisées pour décrire l’état incertain de la matière.
Les conditions aux limites avec le gaz ambiant, la poudre, la matière solidifiée ou le substrat sont pris en compte. L’apport d’énergie du laser est généralement considéré par un terme source venant s’ajouter à l’équation de la chaleur. Il se présente généralement sous la forme d’une gaussienne. Il peut s’agit d’une source surfacique en régime établi, ou volumique en régime transitoire afin de tenir compte de la plus forte pénétration du laser dans la matière.
L’absorption de la poudre est également modélisée. Sans rentrer trop dans les détails la méthode dites du « lancer de rayon » et une résolution des équations de Maxwell permettent de déterminer précisément ce coefficient lors de l’interaction laser-poudre. Cependant une telle méthode est trop lourde et des simplifications sont utilisées pour conserver un temps de calcul acceptable.
Une autre difficulté est la capture des interfaces de transition de phase de la matière (solide, liquide, gaz). Les méthodes mixte Euler/Lagrange ou LevelSet sont les plus couramment utilisées. La principale différence est que, dans le premier cas, les nœuds du maillage doivent être positionnés à l’interface, alors que, dans le second cas, celle-ci est capturée par une fonction composée des distances avec les nœuds situés au voisinage de cette surface. On parle de transport d’interface pour la mise à jour de la position de cette fonction. La méthode LevelSet permet de modéliser l’interface de manière plus précise puisque l’on est pas contraint par le maillage.
Quelque soit la méthode, la capture des phénomènes aux interfaces nécessite d’utiliser des maillages très fins ce qui alourdi considérablement le modèle. Des solutions de remaillage existent cependant.
Par ailleurs, lorsque le phénomène de vaporisation est modélisé, un maillage du domaine complet est nécessaire. Cependant, la plupart du temps ce phénomène est ignoré ou seul l’effet de la vaporisation sur le bain de fusion est modélisé, et non le phénomène lui-même, ce qui permet d’éviter de mailler tout le domaine.
Ces modèles permettent de considérer le régime transitoire lors du passage de la poudre à l’état liquide puis le régime établi lorsque le bain de fusion est formé. Ils permettent de capturer précisément la forme et l’évolution du bain de fusion selon les paramètres laser. Les instabilités de type key-hole ou « balling » sont également correctement prédits.
Cependant les temps de calcul sont de plusieurs heures pour quelques millimètres de cordon de soudure dans le cas d’un mono-cordon. Lorsque plusieurs cordons sont juxtaposés au sein d’une même couche ou en multi-couche, ce type de modélisation devient vite trop lourd pour être utilisée en bureau d’étude.
Des hypothèses simplificatrices et un passage à l’échelle supérieur est envisageable.
Référence :
- Thèse Qiang Chen
- Thèse Alexis Queva
- Thèse Amal Masmoudi
par admin | Nov 10, 2022 | Blog
La simulation numérique permet d’anticiper les problèmes éventuels afin de produire des pièces répondant au cahier des charges et présentant le minimum de défauts. L’idéal étant bien sûr de produire une pièce à la cote du premier coup.
Interaction des trois domaines, thermique, mécanique et métallurgique, entre eux.
La fabrication additive est un procédé multi-physiques par nature : la thermique au sein du bain de fusion et dans la pièce, la mécanique pour la dilatation et les contraintes résiduelles, et enfin la métallurgie pour l’évolution cristallographique du matériau. Ces 3 domaines sont couplés plus ou moins fortement, chacun ayant une influence sur les deux autres. La schéma ci-dessous résume ces interactions.
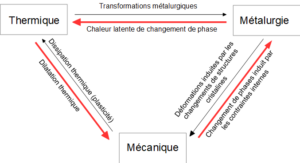
Fig. 1 : Interactions entre les différentes physiques intervenant au cours d’un procédé de fabrication additive métallique. En rouge les interactions prépondérantes ou fortes.
Il faut également distinguer les phénomènes locaux, dits microscopiques, comme les mouvements de convection de la matière fondue au sein du bain de fusion, et les phénomènes globaux, appelés macroscopiques, comme les distorsions de la pièce pendant et après l’impression et retrait des supports. Entre les deux se situent les phénomènes intermédiaires, dits mésoscopiques, comme ceux régissants le comportement des cordons de soudure par exemple.
Lien entre le bain de fusion et le comportement global de la pièce
Du comportement du bain de fusion découle celui du cordon de soudure et la génération de contraintes et déformations en son voisinage. Cet état écroui de la matière, engendré couche par couche, détermine le comportement global de la pièce impliquant les déformations plastiques cumulées et les contraintes résiduelles.
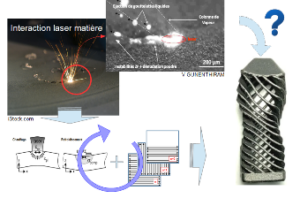
Fig. 2 : Chaine de couplage entre les phénomènes physiques mise ne jeux, de l’échelle du bain de fusion à l’échelle de la pièce
On voit donc que, bien que locaux et contenus dans un volume infime au regard de la taille de la pièce à construire, les phénomènes se produisant au sein du bain ont une influence sur le comportement global de la pièce. Ainsi, l’interaction laser-matière ne peut être réduite à la seule formation du bain de fusion mais doit être appréhender dans sa globalité. Cela nous permet d’introduire progressivement la notion d’échelle et de hiérarchie entre les phénomènes physiques.
Le phénomène prépondérant est la dilatation thermique au voisinage immédiat du bain de fusion. En mode transitoire ou stationnaire, la chaleur se propage dans le substrat ou dans les couches précédemment imprimées. La matière se dilate mais est contrainte par le substrat ou les couches inférieures déjà solidifiées. Il se créé alors des contraintes de compression. A l’inverse, lorsque la matière se refroidie à l’arrière du bain ou lors de la phase de remise en poudre, elle se contracte mais est de nouveau contrainte pas le voisinage immédiat déjà solidifié. Il se créer alors des contraintes de traction.
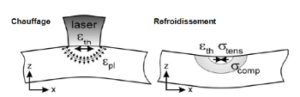
Fig. 3 : Explication de l’apparition des contraintes résiduelles
Du fait des forts gradients thermiques, de chauffage ou de refroidissement, ces contraintes sont extrêmement élevées et dépassent la limite élastique du matériau. Il se créer donc des déformations plastiques permanentes. Une partie de ces déformations seront relâchées lors de la construction des couches supérieures mais se reformeront dans une moindre mesure. C’est la raison pour laquelle on retrouve ces déformations permanentes essentiellement dans le bas de la pièce. Pour la même raison les contraintes résiduelles se concentrent plutôt dans le bas et ne sont pas cumulatives, c’est-à-dire qu’elles n’augmentent pas avec la hauteur de la pièce.
Localement ces contraintes peuvent provoquer l’apparition de micro-fissures. Plus globalement, elles sont également à l’origine de fissures à l’interface avec la plateau par exemple.
Le relâchement d’une partie d’entre elles, lorsque la pièce sera détachée de son support, sera à l’origine des distorsions plus ou moins importantes de la pièce.
Découpage du problème
Plutôt que de chercher à simuler l’ensemble des phénomènes dans un seul et unique modèle, on décline le problème en trois sous-problèmes correspondant généralement à une physique et/ou une échelle bien précise.
1) Échelle micro : c’est l’échelle du bain de fusion. Elle permet de prédire les porosités, l’évolution du bain de fusion, la formation des éjectas, et la vaporisation.
2) Échelle meso : c’est l’échelle du lit de poudre. Elle permet de prédire le manque de fusion, surfusion/vaporisation, les fissurations locales et également la stabilité du bain de fusion.
3) Échelle macro : elle permet de prédire les distorsions pendant et après la fabrication, les risques de collision avec le recoater ainsi que les fissurations.
par admin | Nov 10, 2022 | Blog
Interaction du laser avec le lit de poudre puis avec le bain de fusion
Les électrons d’un laser se comportent comme des grains interagissant avec les particules de matière par le biais de la force électromagnétique. De masse nulle et sans charge électromagnétique ils excitent les électrons des atomes en les faisant changer de niveau d’énergie. Il en résulte une augmentation de la température des atomes ainsi excités. Initialement dans un état énergétique stable, la matière reçoit en quelque sorte l’énergie transportée par les photons du laser.
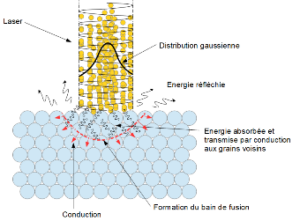
Fig. 1 : Formation du bain de fusion. Interaction des photons avec (les électrons de) la poudre
Les lasers utilisés sont à énergie continue. Le plus répandu est le laser Nd:Yag car sa longueur d’onde plus courte permet une meilleure absorption par la matière. On peut citer également les laser CO2 dont la longueur d’onde est cependant plus élevée.
Une partie de cette énergie est dispersée soit par réflexion du laser sur la matière, soit par interaction du laser avec le gaz issue de la fusion de la poudre. Par ailleurs, l’état de la matière influence également la profondeur de pénétration. A l’état de poudre, le rayon se diffracte sur les particules de poudre et pénètre plus profondément par ses multiples réflexions avec les grains.
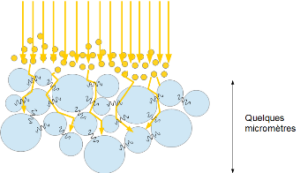
Fig. 2 : Pénétration du laser et réflexion sur les premières couches de grains de poudre
A l’état dense (solide, liquide, pâteux), seuls les électrons libres proches de la surface sont excités et l’échauffement induit se propage dans le reste de la pièce par phénomène de conduction. L’alimentation du bain de fusion se fait par accrétion des grains de poudre situés amont et qui, sous l’effet des forces en présence, sont attirés dans celui-ci.
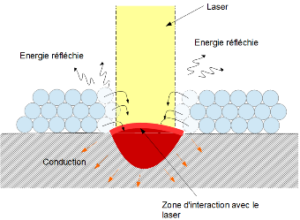
Fig. 3 : Formation du bain liquide de fusion et interaction avec le laser
Régime du bain de fusion
Le comportement du bain de fusion est régi par de nombreux phénomènes : la force de Marangoni, la force de Lorentz, la force de cisaillement aérodynamique et la force de flottabilité. Selon la puissance laser ces forces sont en équilibre stable ou instable donnant lieu à plusieurs régimes de fusion.
Le régime stable se caractérise par un bain bombé sur le dessus et une profondeur de l’ordre de grandeur de l’épaisseur de poudre. Cette forme est due à la tension de surface produite à l’interface bain liquide / gaz. Du fait des forts gradients thermiques à cette interface des forces de Marangoni se mettent en place.
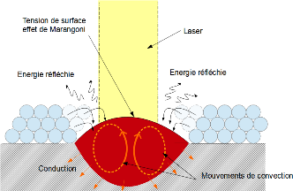
Fig. 4 : Bain de fusion en régime stable
Il existe également un régime de fusion appelé « trou de serrure » ou « keyhole » dans lequel la matière se vaporise et forme un tunnel contre les parois duquel les rayons se réfléchissent et pénètrent ainsi plus en profondeur au sein de la matière.
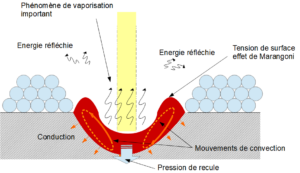
Fig. 5 : Amorce du régime de fusion en mode « keyhole »
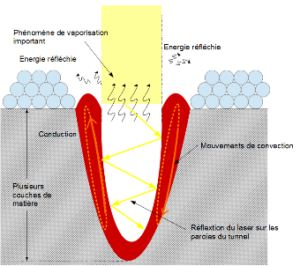
Fig. 6 : Bain de fusion en régime instable ou « keyhole »
Rendement ou absorption d’énergie :
Une partie de l’énergie apportée par le laser est réfléchie et ne participe donc pas à la fusion de la poudre. On appel rendement le pourcentage d’énergie effectivement absorbée et contribuant directement à la la fusion.
Ce rendement est par ailleurs différent selon l’état du bain de fusion. En réalité il varie constamment et est dépendant de la température. Pour simplifier on ne distingue que trois cas : le régime transitoire lorsque le laser entre en contact avec la couche de poudre (début de chaque nouvelle trajectoire), le régime conductif stable et le régime « keyhole » instable.
Références bibliographiques :
- Note CEA
- Thèse Anaïs Baumard
- Thèse Laurent Van Belle (INSA Lyon LaMCos)
- Thèse Alexis Queva (Safran / Université PSL Mines Paris Tech)
- Thèse Qiang Chen (Université PSL Mines Paris Tech)
- Thèse Julie Maisonneuve (Université PSL Mines Paris Tech)
- Thèse Guillaume Marion (Université PSL Mines Paris Tech)
















Commentaires récents